1級土木施工管理技士 過去問
令和7年度
問3 (問題A ユニットa 問3)
問題文
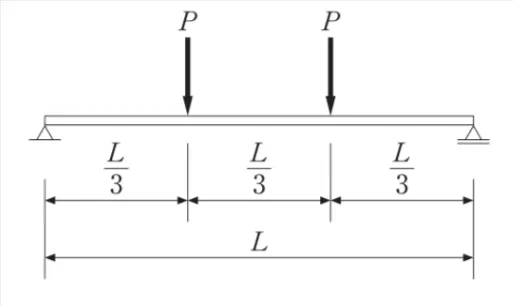
ただし、梁の自重は考慮しないものとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
1級土木施工管理技士試験 令和7年度 問3(問題A ユニットa 問3) (訂正依頼・報告はこちら)
ただし、梁の自重は考慮しないものとする。

正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
この問題で選ぶべきなのは、
両端の支点では曲げモーメントが0で、荷重の間の区間(L/3〜2L/3)が水平のまま一定値になっている図です。
単純梁に左右対称の集中荷重Pが2つ作用した場合、せん断力図から求めた曲げモーメント図は、両端で0、荷重点の間(L/3〜2L/3)で一定となる「台形型」の形になります。
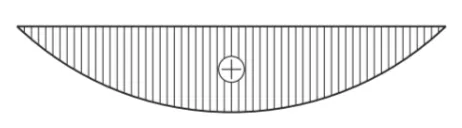
この図は、全体がなめらかな曲線(おわん型)のような形になっています。
このような曲線の曲げモーメント図は、等分布荷重がかかった場合に現れる典型的な形です。
しかし、この問題は「集中荷重Pが2点に作用する場合」です。
集中荷重のときは、せん断力が区間ごとに一定となり、その積分である曲げモーメントは区間ごとに直線になります。
そのため、曲線で表されているこの図は条件に合いません。
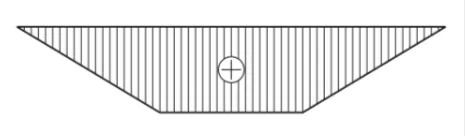
この図は、
支点の位置(両端)で曲げモーメントが0になっている
左端からL/3までは直線で増加
L/3〜2L/3の中央区間では、一定値で水平なまま
2L/3〜右端Lまでは直線で減少し、右端で0になる
という形になっています。
これは、実際につり合い計算とせん断力図から求めた曲げモーメントの性質と一致します。
・反力は左右対称なので
RA=RB=P になります。
・せん断力Vは
0〜L/3:V=+P
L/3〜2L/3:V=0
2L/3〜L:V=−P
となります。
曲げモーメントMは「せん断力Vを区間ごとに積分したもの」なので、
Vが一定(±P)の区間ではMは直線
Vが0の区間ではMは一定値
となります。したがって、
左端からL/3まで直線で増加
L/3〜2L/3は一定
2L/3〜Lで直線で減少
という台形の形が、条件に合う曲げモーメント図になります。
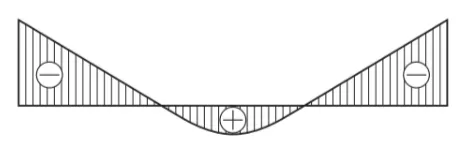
この図は、中央付近で一度下側にへこみ、負の曲げモーメントが生じているような形です。
単純梁に、上向きの反力と下向きの集中荷重だけが作用している場合、
支間内の曲げモーメントは基本的に同じ向き(片側だけ)になります。
この問題のように、梁の上から荷重が2つ作用する条件で、支点以外の位置で曲げモーメントが0を通って符号が変わることはありません。
したがって、中央で負のモーメントを示しているこの図は、荷重状態と合わない図です。
この図は、段々になった「階段状の長方形」のような図で、場所によってモーメントが急に変わっている形です。
しかし、集中荷重が作用しても曲げモーメントは点で飛び跳ねることはありません。
変化のしかたは「傾きが変わる」だけで、値そのものは連続してつながります。
(ジャンプするのはせん断力Vの方です。)
そのため、モーメントが不連続に変化しているように見えるこの図も、曲げモーメント図としては不適当です。
この考え方(まず反力→せん断力図→曲げモーメント図の順で考える)を身につけると、今後の構造力学の問題にも応用しやすくなります。
参考になった数19
この解説の修正を提案する
前の問題(問2)へ
令和7年度 問題一覧
次の問題(問4)へ