1級土木施工管理技士過去問
令和7年度
問4 (問題A ユニットa 問4)

問題文

下図は引張力と引張応力との関係を表しているが、（ア）のように直径Dの部材の両端に軸に沿って離れ合う向きの一対の外力Pが作用しているとき、（イ）のように部材の軸に沿って引張力が生じることとなる。この場合（ウ）のように断面に生じる、引張応力σ_tを表す次の式のうち、正しいものはどれか。問題文の画像

付箋

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

1級土木施工管理技士試験令和7年度問4（問題A ユニットa 問4）（訂正依頼・報告はこちら）

下図は引張力と引張応力との関係を表しているが、（ア）のように直径Dの部材の両端に軸に沿って離れ合う向きの一対の外力Pが作用しているとき、（イ）のように部材の軸に沿って引張力が生じることとなる。この場合（ウ）のように断面に生じる、引張応力σ_tを表す次の式のうち、正しいものはどれか。

正解！素晴らしいです

残念...

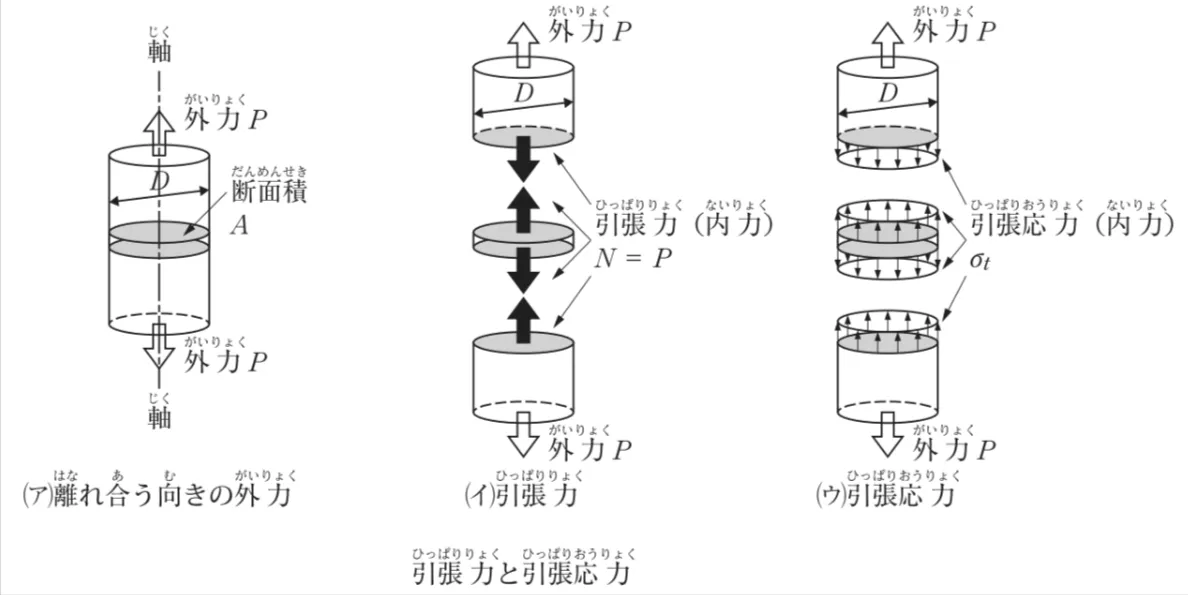
この問題では、直径Dの丸棒に引張力Pが作用したときの引張応力σtを求めます。
正しい式はσt＝4P／πD²です。
理由は、応力は「力÷断面積」で求め、丸断面の面積がA＝πD²／4となるからです。

選択肢1. σ_t＝4P／πD

分母がπDになっていて、Dが2乗されていません。
引張応力は

引張力：P

丸断面の面積：A＝πD²／4

を使って、
σt＝P／A＝P／(πD²／4)＝4P／πD²
となります。

面積にはD²が入るので、Dが1乗のこの式は間違いです。

選択肢2. σ_t＝P／πD

こちらも分母がπDで、Dが2乗されていません。
さらに、PをそのままπDで割っているだけなので、「力÷面積」の形にもなっていません。
単位を考えても、

力P：N（ニュートン）

応力σt：N/mm²

であるべきところ、分母のDが1乗だと次元（単位）のつじつまが合いません。
したがって、この式も不適当です。

選択肢3. σ_t＝4P／πD²

引張応力は
σt＝力P÷断面積A
で求めます。

丸棒の断面は円なので、

直径：D

半径：D／2

より、断面積は
A＝π(D／2)²＝πD²／4
です。

したがって、
σt＝P／A＝P／(πD²／4)＝4P／πD²
となります。

この式は「力÷面積」の形になっており、Dも2乗で入っているので、引張応力σtの式として正しいです。

選択肢4. σ_t＝P／πD²

分母にπD²が入っているので、見た目は「力÷(長さ²)」の形になっていますが、
丸断面の面積A＝πD²／4を使っていない点が問題です。

正しくは
σt＝P／(πD²／4)
なので、分母のπD²に、4が掛かった形（4P／πD²）にならなければいけません。
この式だと、応力の値が本来の4分の1になってしまいます。

まとめ

このように、「応力＝力÷面積」と「円の面積＝π×半径²」の2つをしっかりセットで覚えておくと、他の断面（長方形やリング状など）の応力計算にも応用しやすくなります。

参考になった数4